Measures of position: 위치 측정값 - 백분위수와 사분위수
지금까지 평균과 중앙값과 같은 중심 경향 측정값을 사용하여 데이터의 중심을 설명하는 방법을 배웠다. 또한 표준 편차와 같은 산포도를 사용하여 데이터의 분포를 나타내는 방법도 살펴보았다. 이러한 도구들은 데이터를 탐색하고 이해하는 데 유용하다.
지난글들:
https://g471000.tistory.com/238
https://g471000.tistory.com/239
https://g471000.tistory.com/240
https://g471000.tistory.com/241
이제 위치 측정값을 살펴보면서 기술 통계학의 개념을 완성해 보겠다.
위치 측정값은 특정 값이 데이터셋 내에서 다른 값들과 비교하여 어느 위치에 있는지를 결정하는 데 도움이 된다. 중심 경향과 분포도를 함께 고려할 때, 개별 값들의 상대적인 위치를 파악하는 것이 중요하다. 예를 들어, 어떤 값이 다른 값보다 높은지 낮은지, 또는 데이터셋의 하위, 중위, 상위 부분에 속하는지를 아는 것이 유용하다.
백분위수(Percentile)

백분위수(percentile)는 데이터 값 중에서 특정 백분율 이하에 해당하는 값을 의미한다. 백분위수는 데이터를 100개의 동일한 부분으로 나누어 특정 값의 상대적 위치를 나타낸다.
예를 들어, 표준화된 시험 점수는 백분위수를 사용하여 수험생의 성취도를 비교할 수 있다. 시험 점수가 99번째 백분위수에 해당한다면, 이는 해당 점수가 전체 응시자의 99%보다 높은 점수라는 의미이다. 마찬가지로 50번째 백분위수에 속하는 점수는 전체 점수의 절반보다 높은 점수임을 나타낸다.
중요한 점: 백분위수와 백분율(%)은 서로 다른 개념이다. 예를 들어, 시험에서 100점 만점에 90점을 받아 90%를 기록했다고 해서 90번째 백분위수에 해당하는 것은 아니다. 백분위수는 전체 응시자들의 성적 분포를 기준으로 결정된다. 만약 전체 응시자의 절반이 90점 이상을 받았다면, 90점은 50번째 백분위수에 속할 수 있다.
예제: 연비 비교
미국에서 연비는 1갤런당 주행 가능한 마일(mpg)로 측정된다. 특정 중형 세단이 23mpg의 연비를 가졌다고 가정해 보자. 이 값이 25번째 백분위수에 해당한다면, 이는 전체 중형 세단 중 75%가 더 높은 연비를 가지고 있다는 의미이다.
사분위수(Quartile)

사분위수(quartile)는 데이터셋을 네 개의 동일한 부분으로 나누는 값이다.
- Q1 (제1사분위수): 데이터의 하위 25%를 포함하는 값 (25번째 백분위수)
- Q2 (제2사분위수, 중앙값): 데이터의 중간값 (50번째 백분위수)
- Q3 (제3사분위수): 데이터의 상위 25%를 포함하는 값 (75번째 백분위수)
각 사분위수는 데이터의 상대적 위치를 비교하는 데 유용하다.
예제: 자동차 판매 데이터
어떤 자동차 판매점에서 지난달 각 영업사원이 판매한 차량 대수를 분석한다고 가정해 보자.
| 영업사원 | 판매 차량 수 |
| #1 | 18 |
| #2 | 13 |
| #3 | 6 |
| #4 | 10 |
| #5 | 15 |
| #6 | 7 |
| #7 | 10 |
| #8 | 9 |
사분위수를 구하는 과정은 다음과 같다.
- 데이터를 오름차순으로 정렬한다: 6, 7, 9, 10, 10, 13, 15, 18
- 중앙값(Q2)을 찾는다: 10과 10의 평균값이므로 Q2 = 10
- 하위 절반(6, 7, 9, 10)의 중앙값(Q1)을 찾는다: (7 + 9) / 2 = 8
- 상위 절반(10, 13, 15, 18)의 중앙값(Q3)을 찾는다: (13 + 15) / 2 = 14
이러한 분석을 통해 영업사원의 성과를 비교할 수 있다.
- Q1(8) 이하의 영업사원은 전체 중 25%에 해당한다.
- Q3(14) 이상의 영업사원은 상위 25%에 해당한다.
- 중간 50%의 영업사원은 8~14대의 차량을 판매했다.
사분위 범위 (IQR)
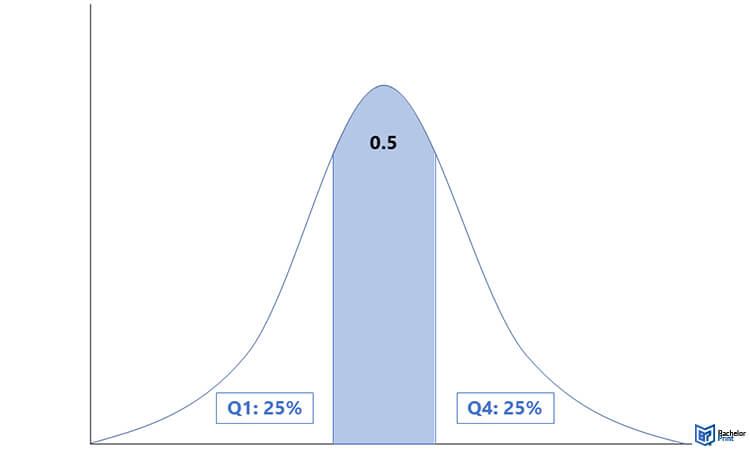
사분위 범위(interquartile range, IQR)는 데이터의 중간 50%가 얼마나 퍼져 있는지를 나타내는 값으로, 다음과 같이 계산된다.
IQR = Q3 - Q1
위의 자동차 판매 데이터를 적용하면:
IQR = 14 - 8 = 6
IQR은 이상값을 식별하는 데 유용하다. 일반적으로 다음 범위를 벗어나는 값은 이상값으로 간주할 수 있다.
Q1 - (1.5 * IQR) 이하 또는 Q3 + (1.5 * IQR) 이상인 값
다섯 숫자 요약 (Five-Number Summary)

다섯 숫자 요약(five-number summary)은 데이터 분포를 요약하는 주요 지표를 포함한다.
- 최솟값 (Minimum)
- 제1사분위수 (Q1)
- 중앙값 (Q2, Median)
- 제3사분위수 (Q3)
- 최댓값 (Maximum)
자동차 판매 데이터의 다섯 숫자 요약은 다음과 같다.
최솟값: 6
Q1: 8
중앙값 (Q2): 10
Q3: 14
최댓값: 18
핵심 정리
- 백분위수(Percentile)는 데이터에서 특정 값의 상대적 위치를 나타낸다.
- 사분위수(Quartile)는 데이터를 네 개의 구간으로 나누어 비교할 수 있도록 한다.
- 사분위 범위(IQR)는 중간 50%의 분포를 측정하며 이상값 탐색에 유용하다.
- 다섯 숫자 요약(Five-Number Summary)은 데이터의 주요 분포 특성을 요약하는 방법이다.
데이터 분석가들은 이러한 위치 측정값을 활용하여 교육, 비즈니스, 공공 건강 등 다양한 분야에서 데이터를 해석하고 비교한다.
참고자료
더 자세한 내용을 알고 싶다면 Freie Universität Berlin의 통계 사전을 참고하면 유용한 정의와 예시를 확인할 수 있다.