Cost Function (비용함수) | Supervised Machine Learning: Regression and Classification

Coursera Machine Learning Specialization > Supervised Machine Learning: Regression and Classification > Introduction to Machine Learning

 

선형 회귀를 구현하려면 Cost Function(비용 함수)를 정의하는게 첫번째 단계이다. 비용함수를 이용해 이 모델이 얼마나 잘 동작하는지 알 수 있다. 예를 들어 다음과 같은 선형(Linear) Regression 모델이 있다고 가정해보자.

 

$ Model: f(x) = wx + b $

 

여기서 w와 b를 parameters인데, 머신러닝에서는 이 변수들을 변경해갈 수 있다. 머신러닝은 이 파라미터를 coefficients 또는 weights라고 부른다. 선형 함수에서는 이 w,b값에 따라 아래와 같이 다른 그래프를 그릴 수 있게 된다.

https://youtu.be/CFN5zHzEuGY?si=ur0caPKaUdBUJzmA

 

 

Linear Regression은 많은 데이터를 가장 잘 나타낼 수 있는 선을 그리는 것인데,

https://youtu.be/CFN5zHzEuGY?si=ur0caPKaUdBUJzmA

 

여기서 내가 그린 선과 각 데이터들과의 차이를 모두 종합해서 보여주는것이 바로 Cost Function 이라고 할 수 있다. 위 예제를 보면, 처음 포인트는 꽤 선과 근접해서 오차값이 별로 없지만, 두번째 X는 아래로 조금 떨어져 있고, 세번째 X는 상당히 많은 차이를 보이고 있다. 이렇게 각 점마다 선에 근접하다면, 우리가 그린 선(모델)이 실제 값들에 근접하다고 할 수 있는데, 이것을 수학적으로 얼마나 근접한지 나타내는게 바로 Cost Function이다. 수식은 아래와 같다.

복잡해 보이지만, 하나하나 살펴보면 간단하다. 즉, 함수에서 y값을 찾고, 그 값에서 실제 그 자리의 y값을 빼준 후 제곱을 한다. 예를 들어, (1,1) 인 값이 있는데, 우리 모델은 (1,3)의 점을 포함하는 선을 그렸다면, 그 차이는 (3 - 1)인 2 이고, 그것의 제곱을 하면 4가 된다. 이런 식으로 모든 점들마다 모델(선)이 그린 값과 비교 하고 제곱해서, 모든 오차들을 합한것을 갖고 비교를 하게 되는데, 이것을 m(값의 갯수) 또는 2m으로 나눠서 조금더 값이 깔끔하게 보이도록 하기도 한다.

 

 

Summary 

정리를 하자면 위와 같다. 선형회귀모델(Linear Regression Model) 이라는 것은 f(x) = wx + b와 같다. 이중 파라미터(coefficent, weight으로도 불린다)는 w와 b이고, 이 값들을 조정해 가면서 주어진 값들과 가장 가까운 선을 하나 그리는 것이 바로 Linear Regression Model Training이다. 여기서 "값들과 가깝다"라는 것을 어떻게 알 수 있을까? 바로 Cost Function을 이용하는 것이다. 선과 실제 값의 위치 차이를 제곱하고, 그것을 모두 다 더해서 값의 갯수 (또는 갯수 곱하기 2)로 나눠주는 값을 찾고, 이것을 J(w, b)라고 말한다. 여기서 최적의 모델을 찾는다는 목표는, 이 J(w,b)이 최대한 작은것을 찾는것이다.

 

 

 

이 예시는 w를 0.5로 하고 b가 0일때의 예시인데, 우리가 가진 값들과 꽤 가까운것을 볼 수 있다. 이 오차값을 Cost Function을 이용해서 계산했더니 0.58이 나왔다.

 

 

이번에는 w=0인 선을 그렸다. 오차값이 2.3이 나왔고, 이는 위의 예시보다 훨씬 크다. 그래서 이 선(Linear)은 좋은 모델이 아니라고 할 수 있다. 이런 식으로 모든 w값들에 대해(예시에서는 단순화 시키기 위해 b를 0으로 세팅했다) 오차 값을 계산해서, 가장 오차값이 적은 값을 찾아내는 과정이 바로 트레이닝 이다. 위 예시를 보면 어떤 값이 w가 되었을 때, 가장 오차값이 적을까? 바로 w = 1 일때 이다.

 

w = 1 인 그래프를 그리게 되면, J(w) 값이 가장 minimum이므로 우리의 목표에 알맞다. 즉, 우리는 아래와 같은 모델을 만들 수 있다.

 

$ f(x) = x $

 

 

J(w, b)

위의 예시는 조금더 간단한 예시를 갖고 학습했다면, 이번에는 함수에 w, b값이 모두 있을 경우를 알아보았다.

https://youtu.be/bFNz2u0hl9E?si=fbW4gfYjUXehq_dq

빨간 x로 표시된 값들을 잘 표현하는 w와 b를 찾아내는 과정을 거쳐서 가장 좋은 성능을 보이는 Funciton을 찾아야한다. 위 예시에서는 w가 0.06, b가 50인 선을 그렸다. 그리고 우리의 목표는

 

 

j와 w값을 변경해 가면서 J(w,b) 값이 가장 작은 어떤 위치를 찾아내는 것 이다. 위 3D 그래프에서 볼 수 있듯, 아래쪽으로 가면 보라색으로 되어있는 부분이 미니멈 값에 가깝고, 그 중 가장 작은 위치를 찾아, 그에 해당하는 w와 b를 찾아 내는것이 우리의 목표이다.

 

예시를 한번 보자. 아래와 같은 함수를 트레이닝 도중 그리고, 얼마나 성능이 좋은지 파악한다고 가정해보자.

 

$ f(x) = -0.15x + 800 $

 

이는 w가 -0.15이고, b가 800인 선이고, 이 선을 이용해서 실제 값과 거리 차이를, Cost Function을 이용해 계산하게 된다. 그렇게 찾아낸 J(-0.15, 800)은, 오른쪽 상단에 보여지는 Visualization에서 볼 수 있듯, Minimum에는 한참 못 미치는것을 알 수 있다. 눈으로 보기에도, 모델(선)과 값들이 한참 떨어져 있음을 알 수 있다.

 

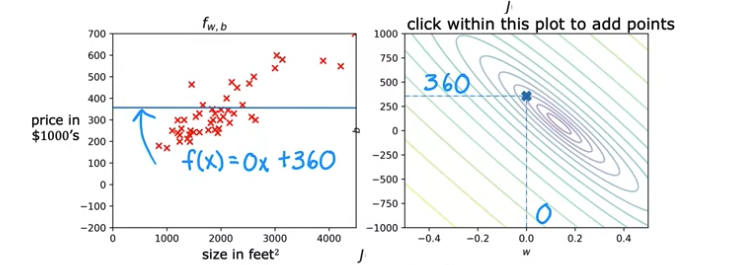
수평선을 그려본 모델을 한번 살펴보자. 이 전의 예측 모델보다는 그나마 가까운 포인트가 많아졌다. 하지만 J(0, 360)을 살펴보면, 아직 Minimum 값에서 조금 떨어져있는것을 알 수 있다. 이전 보델보다는 가깝지만, 육안으로 보기에도, 아직 떨어져있는 포인트들이 많이 보인다.

많은 시도 끝에, 이런 모델을 그려냈다고 해보자. w가 0.13, b가 71인 f(x)이고, 이 오차값을 계산 했을 때, J(0.13, 71)은 minimum값을 갖는다. 그러므로 이 선형회귀모델(Linear Regression Model)을 최종 모델로 선정하고 사용하는것이 다른 모델들보다 유리할것으로 판단된다.

 

 

 

 

Reference

https://youtu.be/CFN5zHzEuGY?si=ur0caPKaUdBUJzmA

 

https://youtu.be/peNRqkfukYY?si=7F2m7B1Qh10qV4-7

 

https://youtu.be/bFNz2u0hl9E?si=wGWrDTfzvSqkQbUf

https://www.youtube.com/watch?v=L5INhX5cbWU&list=PLkDaE6sCZn6FNC6YRfRQc_FbeQrF8BwGI&index=14