지도학습 | K-NN Regression (최근접 이웃 회귀)

KNN을 이용해서 Regression문제도 풀어낼 수 있다. KNN을 이용하게 되면, 예측값은 가장 가까운 이웃의 타겟값이 된다. 

!pip install mglearn
import mglearn

mglearn.plots.plot_knn_regression(n_neighbors=1)

 

이렇게 하면, 가장 가까운 이웃 1개를 골라서 그것이 결과값이 된다. 결과는 다음과 같았다.

 

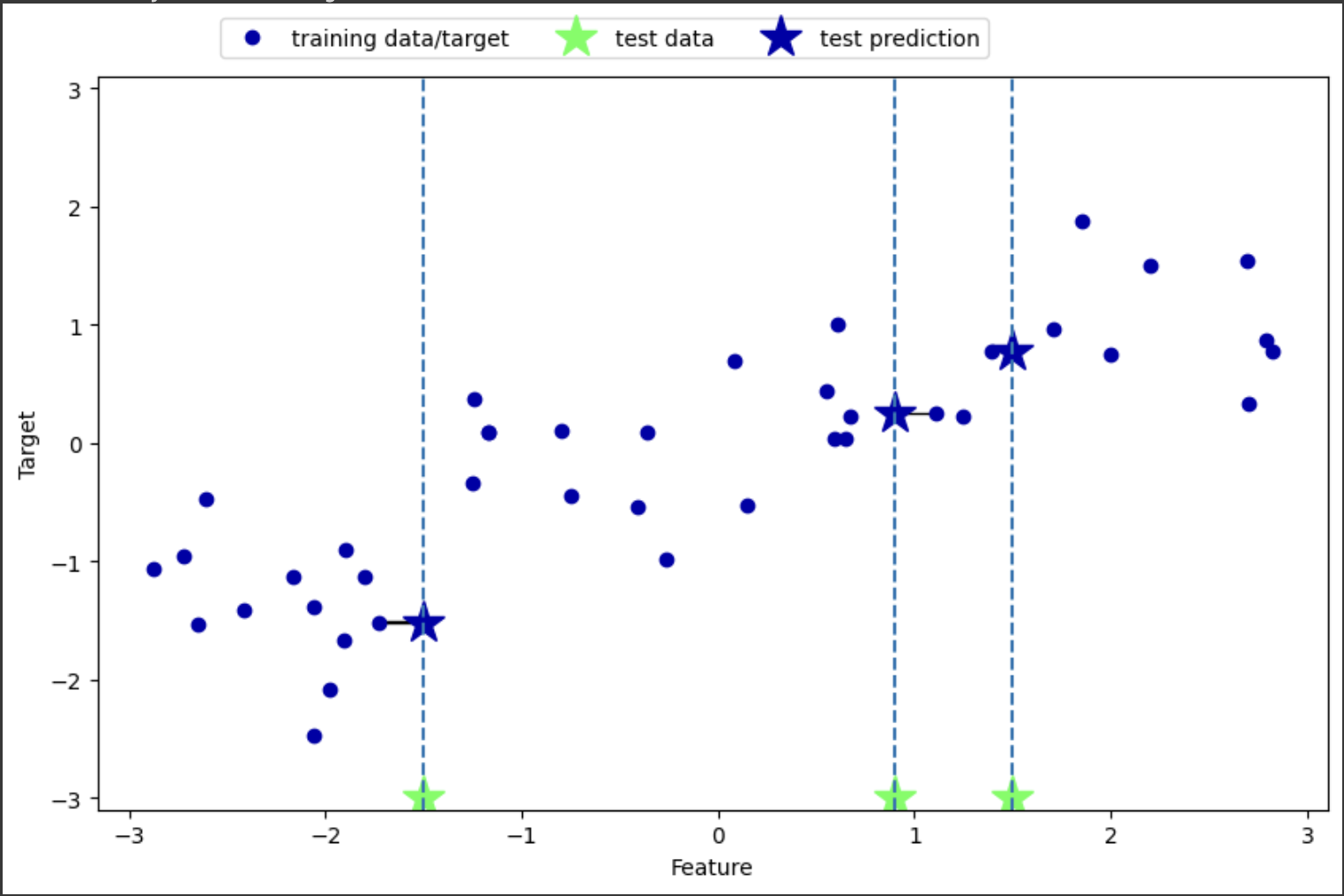
각 인풋(test data)별로, 가장 가까운 데이터(training data/target)을 찾아내고, 그 타겟을 결과값으로(test prediction) 나타내었다. 여기서 K-NN은, 1-NN이었는데, 코드를 조금 수정해서 K를 1보다 큰 숫자를 사용해 회귀분석을 할 수 있다. 

mglearn.plots.plot_knn_regression(n_neighbors=3)

 

3-NN

위와 비슷하지만, 가장 근접한 3개를 찾아서 평균값을 찾아내 예측을 했다. 

 

scikit-learn에서 Regression을 위한 KNN 알고리즘은 KNeighborsRegressor에 구현되어있다. 사용법은 아래와 같다.

from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split

X, Y = mglearn.datasets.make_wave(n_samples=40)

# wave 데이터셋을 train/test 세트로 나눈다.
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0) 

# 이웃의 수를 3개로 한 3-NN 모델 객체를 만든다.
reg = KNeighborsRegressor(n_neighbors=3)

# test/target 데이터를 사용해 모델을 학습시킨다.
reg.fit(X_train, Y_train)

 

 

이제 , 트레이닝한 모델을 이용해 테스트 세트를 예측해보자.

# 테스트 세트를 예측한다. 또 Y값도 프린트 해보자.
print("테스트 세트 예측:\n", reg.predict(X_test))
print("테스트 세트 실제값:\n", Y_test)

# 테스트 세트의 score를 계산한다.
print("테스트 세트 R^2: {:.2f}".format(reg.score(X_test, Y_test)))

 

테스트 세트 예측: [-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382 0.35686046 0.91241374 -0.44680446 -1.13881398]
테스트 세트 실제값: [ 0.37299129 0.21778193 0.96695428 -1.38773632 -1.05979555 -0.90496988 0.43655826 0.7789638 -0.54114599 -0.95652133]
테스트 세트 R^2: 0.83

 

score 함수를 이용해 모델을 평가했다. Regression의 경우 R^2값을 반환한다. 점수는 0.83으로 비교적 잘 맞았다고 볼 수 있다.

 

 

장단점과 매개변수

KNN Classification에서 매개변수는 두가지이다. 데이트 포인트 사이의 거리를 재는 방법과 이웃의 갯수이다. 실제 이웃의 수는 3-5개정도로 적을 때 잘 작동하고, 거리는 재는 방식은 보통 유클리디안 방식(Euclidean distance)을 사용한다. 

 

KNN의 장점은 이해하기 매우 쉬운 모델이며 많이 조정하지 않아도 쉽게 좋은 성능을 발휘한다는 점이다. 아주 복잡한 알고리즘들을 사용하기 전, 시도해볼 수 있는 좋은 시작점이다. 하지만, 빠르게 만들 수 있다는 장점과 반대로, 훈련세트가 매우 크면 예측이 느려진다. KNN을 사용할 땐, 데이터 전처리 과정이 아주 중요하다. 

 

그리고, 수백개 이상의 특성을 가진 데이터셋 또는 Feature값 대부분이 0인 데이터셋과는 특히나 잘 동작하지 않는다.

 

KNN알고리즘은 쉽지만, 예측이 느리고 많은 특성을 처리하는 능력이 부족해, 현없에서 많은 케이스에는 쓰여지지 않는다. 이런 단점이 많이 없는 알고리즘이, 다음에 공부할 Linear Regression, 즉 선형 모델이다.

 

 

Reference

https://colab.research.google.com/drive/1fzSiPpwbTUplw6G0PJSpGaVBWx5CEMIZ?usp=sharing

_02_supervised_machine_learning.ipynb

https://www.yes24.com/Product/Goods/42806875

파이썬 라이브러리를 활용한 머신러닝 - 예스24

https://en.wikipedia.org/wiki/Euclidean_distance

Euclidean distance - Wikipedia