-
Cost Function for Logistic Regression (로지스틱 회귀를 위한 비용함수) | Supervised Machine Learning: Regression and ClassificationMachine Learning/Stanford ML Specialization 2023. 11. 6. 20:37
Squared Error Cost
Classification Model을 생성하기 위해서는 Logistic Regression을 이용해서 예측할 수 있다고 배웠다. 그렇다면, 다른 모델들처럼 생성된 모델의 성능을 평가할 수 있어야한다. Logistic Regression의 Cost Function이 무엇인지 알아보자.
다음과 같은 트레이닝 데이터셋이 있다고 가정하자.
Tumor Size (cm) ... patient's age malignant? 10 52 1 2 73 0 5 55 0 12 49 1 ... ... ... training example은 1부터 m까지, feature은 1부터 n까지 존재한다고 해보자. 또한 target은, malignant column이 보여준 것 처럼 y 이다. 그렇다면, 아래 공식을 다시 살펴보자.

https://youtu.be/vq4Ie5xWhww 여기서 우리는 0 과 1들의 위치를 잘 나타내는 sigmoid 함수를 만들어야하는데, 여기서 w와 b 값을 어떻게 선택할 수 있을까? 다른 모델들처럼 이 값들을 바꿔줘 가면서, 가장 성능이 좋은 값을 찾아내야만 한다. Linear Regression처럼 Squared Error Cost는 어떨까?

https://youtu.be/vq4Ie5xWhww 좋은 선택은 아니다. 우선적으로 비볼록(non-convex)함수가 그려져서, 어떤게 적절한 minimum인지 알 수 없는 그래프가 그려진다. 이럴 경우 local minimum, 즉, 지역 최솟값에 갇힐 수 있다. 즉, 실제 minimum이 아닌데, minimum으로 계산될 수 있다. 또한, 이 Squared Error Cost는 이상치, Outliers에 민감하다. 이상치가 있는 경우에 모델 학습에 큰 영향을 미칠 수 있고, 예측력도 약화 시킬 수 있다. 또한 로지스틱 회귀의 출력은 0 또는 1 사이의 값을 갖는데, Squared Error Cost(제곱 오차 비용)함수를 사용하게 되면, 이 범위를 벗어나는 오차가 발생할 수 있다고 한다. 그러면 어떤 방식이 좋을까?
Logistic Loss Function
바로 log를 활용한 방법으로 Loss Function을 생성해서 사용할 수 있다. Classfication의 특성 때문에, Class의 True(1), False(0)에 따라서 식은 달라진다.

https://youtu.be/vq4Ie5xWhww 먼저, i번째 y가 1, 즉 종양이 악성(양성)일 경우를 살펴보자. 즉, 실제 값은 1, True일 때, 모델 f(x) 의 값이 예측을 100%라고 했다면? 왼쪽 아래 그래프를 보자. -log(f)의 그래프이다. 만약, f(x)의 값이 1에 가깝다면, y축은 0으로 향한다. 즉, error rate가 아주 적은것이다. 만약 0.5라고 예측한다면? 1일때보다는 많이 커진다. 만약, 0.1 또는 그보다 작은 수가 예측된다면? 이는 예측을 완전히 빗나간 것 이다. y축도 0.1에는 많이 상승해 있는 것을 볼 수 있다. 즉, 예측 값이 작아지면 작아질수록, error 값은 무한대로 커진다.
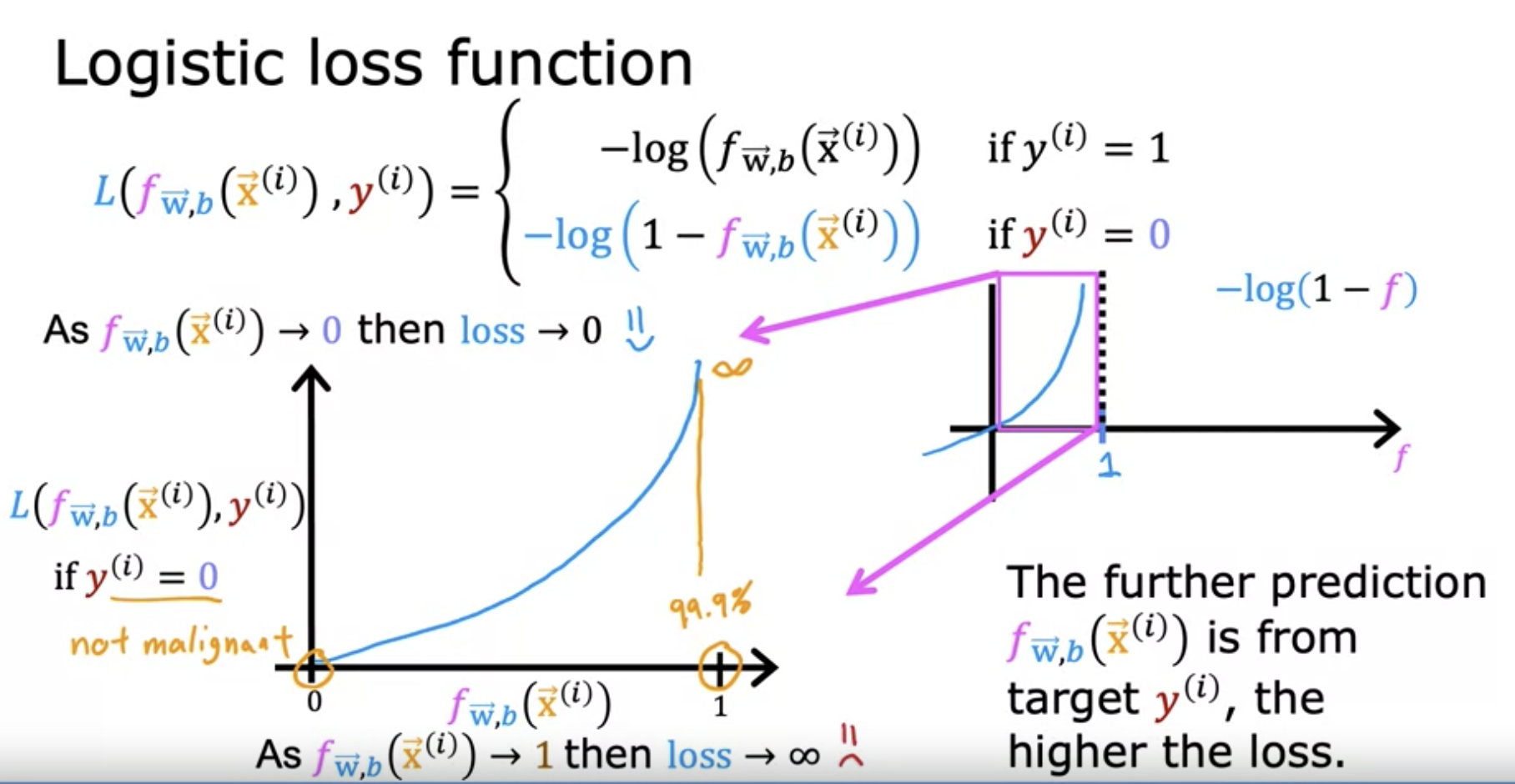
https://youtu.be/vq4Ie5xWhww 이번에는 실제 값이 0, 즉 종양이 음성일 경우를 살펴보자. 실제 값은 0, False일 때, 모델 f(x)의 값이 예측을 0%라고 했다면, 이는 아주 훌륭한 예측이다. 종양일 가능성이 없다고 잘 예측한 것이기 때문이다. 이렇게 실제 값이 0인 데이터에게는 조금 다른 로그 함수가 적용되는데, 방식은 이전과 같다. 바로 -log(1 - f)의 함수이다. 위 그래프를 보면 알 수 있듯, 형태는 비슷하지만, 거울모드를 적용한 것 같다. 이는 당연하다. 만약, 실제값이 0인데, 예측도 0으로 했다면? Error Rate는 0이다. 만약, 99.9%로 예측 했다면? 이는 무한대에 가까워지는 값을 내고, 이 모델은 성능이 아주 좋지 않다는것을 알아낼 수 있다.
이렇게 각각 수식의 Loss Function을 알아봤는데, 총 Cost는 이 것들을 모두 합쳐서, Testing Set의 갯수로 나누어주면 된다. 즉, 모든 Loss Function의 아웃풋들의 평균을 계산하면 된다.

https://youtu.be/vq4Ie5xWhww Simplified Cost Function
이 Cost Function을 따로 나눠서가 아니라, 한 수식으로 쓸 수 있다.

https://youtu.be/YkTcK_LXAxw 우리는 y의 값이 1 또는 0인것을 안다. 위의 예시처럼 수식을 합쳐놓으면, 따로 계산하지 않아도 알아서 반대 항이 사라진다. 예를 들어보자. 만약 y = 1이라면, 오른쪽에 있는 (1 - y) 가 0이 되므로, 오른쪽은 사라지고, -log(f(x))만 남게 된다. 또한 y = 0일 경우, 왼쪽 항은 사라지고, -log(1 - f(x))만 남게 되어서, 원래의 의도대로 계산할 수 있게 된다. Cost Function역시 이것을 이용해서, Loss Function을 따로 생략하지 않고 위와 같이 나타낼 수 있다.
Reference
'Machine Learning > Stanford ML Specialization' 카테고리의 다른 글