Normal Distribution: 정규 분포

지금까지 우리는 실험의 결과가 셀 수 있는 정수로 표현되는 이산 확률 분포(Discrete Probability Distribution)에 대해 이야기했다. 예를 들어, 주사위를 굴리면 결과는 2 또는 3이 될 수 있지만, 2.178이나 3.394 같은 소수 값이 나올 수는 없다.

 

이제 연속 확률 분포(Continuous Probability Distribution)로 넘어가 보자. 연속 확률 분포는 특정 구간 내에서 모든 값을 가질 수 있는 확률 분포를 의미한다. 일반적으로 키, 몸무게, 시간, 온도와 같은 측정 가능한 변수가 이에 해당한다. 예를 들어, 시간을 측정할 때 소수 자릿수를 계속 추가하여 더 정밀하게 측정할 수 있다.

 

이번 글에서는 가장 널리 사용되는 확률 분포 중 하나인 정규 분포(Normal Distribution)에 대해 알아보겠다.

 

정규 분포(Normal Distribution)란? 

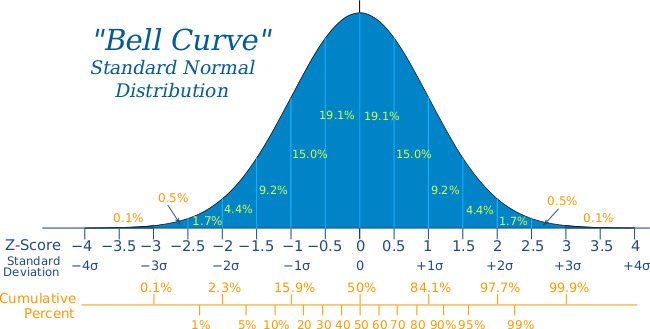
https://www.mathsisfun.com/data/standard-normal-distribution.html

 

정규 분포는 연속 확률 분포 중 하나로, 좌우 대칭의 종 모양(Bell Shape)을 가진다. 이러한 형태 때문에 벨 곡선(Bell Curve)이라고도 불린다. 또한, 이 분포를 처음으로 수식화한 독일 수학자 카를 프리드리히 가우스(Carl Friedrich Gauss)의 이름을 따서 가우스 분포(Gaussian Distribution)라고도 한다.

정규 분포는 다음과 같은 특징을 가진다:

1. 평균(mean, μ)이 분포의 중심이며, 곡선의 가장 높은 지점이다.
2. 곡선은 대칭적이며, 평균을 중심으로 좌우가 동일하다.
3. 평균에서 멀어질수록 값이 나올 확률이 낮아진다.
4. 곡선 아래 면적의 총합은 1이다.

많은 데이터 세트가 정규 분포를 따른다. 예를 들어, 100명을 무작위로 선택하여 신장을 측정하면 신장은 정규 분포 곡선을 따르는 경향이 있다.

 

표준화 시험에서도 대부분의 사람들은 평균 근처의 점수를 받는다. 평균보다 훨씬 낮거나 높은 점수를 받는 사람은 소수에 불과하다. 이렇게 데이터가 평균을 중심으로 분포하는 경우, 정규 분포 곡선이 생성된다.

 

정규 분포의 그래프 이해하기

정규 분포에서 X축은 측정하고자 하는 변수의 값(예: 시험 점수), Y축은 해당 값이 나타날 확률을 나타낸다.

사과의 무게가 평균 100g, 표준편차 15g으로 정규 분포를 따른다고 가정하면 다음과 같은 특징을 가진다.

• 평균(μ): 100g
• 표준편차(σ): 15g

이 경우, 정규 분포 그래프는 다음과 같다.

1. 곡선의 중심(최고점)은 평균인 100g에 위치한다.
2. 곡선은 평균을 기준으로 좌우 대칭이다.
3. 평균에서 멀어질수록 발생 확률이 감소한다. 즉, 100g보다 크게 벗어난 무게(예: 55g 또는 145g)는 발생 확률이 낮다.
4. 곡선 아래 면적의 총합은 1이며, 이는 모든 가능한 사과 무게의 확률을 합하면 100%가 된다는 뜻이다.

 

표준편차와 경험적 법칙(Empirical Rule)

표준편차(Standard Deviation, σ)란?

표준편차(σ)는 데이터가 평균(μ)으로부터 얼마나 떨어져 분포하는지를 측정하는 값입니다.
즉, 데이터가 평균 주변에서 얼마나 퍼져있는지를 나타내는 척도입니다.

• 표준편차가 작을 경우 → 데이터가 평균 근처에 몰려 있음 (분포가 좁고 뾰족함)
• 표준편차가 클 경우 → 데이터가 평균에서 멀리 퍼져 있음 (분포가 넓고 완만함)
•  

 

예를 들어, 사과의 무게가 정규 분포를 따르고,
평균(μ) = 100g, 표준편차(σ) = 15g이라면:

• 평균에 가까운 값(100g)은 많이 나타날 확률이 높음
• 평균에서 멀어질수록(예: 55g, 145g) 나타날 확률이 낮아짐

 

경험적 법칙(Empirical Rule, 68-95-99.7 Rule)

경험적 법칙은 정규 분포에서 데이터가 표준편차를 기준으로 어떻게 분포하는지를 나타내는 규칙입니다.

정규 분포에서, 전체 데이터의

• 68%가 평균 ±1σ (한 표준편차) 안에 있음
• 95%가 평균 ±2σ (두 표준편차) 안에 있음
• 99.7%가 평균 ±3σ (세 표준편차) 안에 있음

사과 무게 예제 적용하기

• 평균(μ) = 100g, 표준편차(σ) = 15g일 때:
  • 68%의 사과는 85g ~ 115g 범위에 속함
  • 95%의 사과는 70g ~ 130g 범위에 속함
  • 99.7%의 사과는 55g ~ 145g 범위에 속함

즉, 대부분의 사과(약 95%)는 70g에서 130g 사이의 무게를 가짐을 알 수 있습니다.

 

 

실제 활용 예시

시험 점수 예시 (평균 = 70점, 표준편차 = 10점)

• 68%의 학생이 60점 ~ 80점 사이에 위치 (1σ 범위)
• 95%의 학생이 50점 ~ 90점 사이에 위치 (2σ 범위)
• 99.7%의 학생이 40점 ~ 100점 사이에 위치 (3σ 범위)
• 40점 이하 또는 100점 이상을 받은 학생은 매우 드물게 발생 (이상치)

공장 제품 품질 관리 예시 (평균 = 500g, 표준편차 = 5g)

• 68%의 제품이 495g ~ 505g 사이에 위치 (1σ 범위)
• 95%의 제품이 490g ~ 510g 사이에 위치 (2σ 범위)
• 99.7%의 제품이 485g ~ 515g 사이에 위치 (3σ 범위)
• 485g 이하이거나 515g 이상인 제품은 불량품일 가능성이 큼

 

표준편차의 역할

• 평균은 데이터의 중심을 나타내고, 표준편차는 데이터가 평균에서 얼마나 퍼져 있는지를 나타낸다.
• 표준편차가 크면 데이터가 평균에서 더 넓게 분포하고, 표준편차가 작으면 데이터가 평균 주변에 더 집중된다.

 

예를 들어, 사과의 평균 무게가 100g이고, 표준편차가 15g인 경우:

• 평균보다 1 표준편차 위(μ + σ): 115g
• 평균보다 1 표준편차 아래(μ - σ): 85g
• 평균보다 2 표준편차 위(μ + 2σ): 130g
• 평균보다 2 표준편차 아래(μ - 2σ): 70g

 

경험적 법칙(Empirical Rule)

경험적 법칙은 정규 분포에서 값들이 평균을 중심으로 어떻게 분포하는지 설명하는 법칙이다.

 

경험적 법칙에 따른 데이터 분포

• 68%의 데이터가 평균 ±1 표준편차 범위 내에 존재
• 95%의 데이터가 평균 ±2 표준편차 범위 내에 존재
• 99.7%의 데이터가 평균 ±3 표준편차 범위 내에 존재

 

사과 무게 예제에서

• 68%의 사과는 85g ~ 115g 범위에 있음
• 95%의 사과는 70g ~ 130g 범위에 있음
• 99.7%의 사과는 55g ~ 145g 범위에 있음

이 법칙을 사용하면 대략적인 데이터 분포를 빠르게 예측할 수 있다.

 

마무리

정규 분포는 비즈니스, 과학, 정부, 머신러닝 등 다양한 분야에서 데이터 분석의 핵심 도구로 사용된다.

• 정규 분포는 종 모양의 대칭 곡선을 가진다.
• 평균이 중심이며, 표준편차는 데이터의 퍼짐 정도를 나타낸다.
• 경험적 법칙을 활용하면 데이터 분포를 빠르게 파악할 수 있다.
• 머신러닝 모델과 통계 분석에서 정규 분포를 가정하는 경우가 많으므로, 이를 이해하는 것이 중요하다.