Regularized Linear Regression(정규화 선형 회귀) | Supervised Machine Learning: Regression and Classification

Coursera Machine Learning Specialization > Supervised Machine Learning: Regression and Classification > Classification

 

앞에서 배운 Regularization을 이용해서 Linear Regression에 적용하면 어떻게 될까? 정규화 선형 회귀(Regluarized Linear Regression)을 위한 경사 하강법(Gradient Descent)에 대해서 알아보자. b값에 대해서는 Regularization을 할 필요 없기때문에, 아래 수식을 반복해서 경사하강을 진행하면 된다.

 

https://youtu.be/jhrrw8Iuus0

 

기존의 수식에서 w값을 업데이트 할 때, Squared Error Cost 뿐만 아니라, Loss Function을 이용해서 Regularization까지 고려한 계산으로 업데이트해서 w값을 지속적으로 바꿔나가주면, 앞에서 커버한 대로, 값을 맞추는것 뿐만 아니라, 추후 다른 값들도 수용할 수 있는 모델을 만드는데 도움이 된다.

 

여기서 이 수식이 어떻게 계산 되는지 살펴보자.

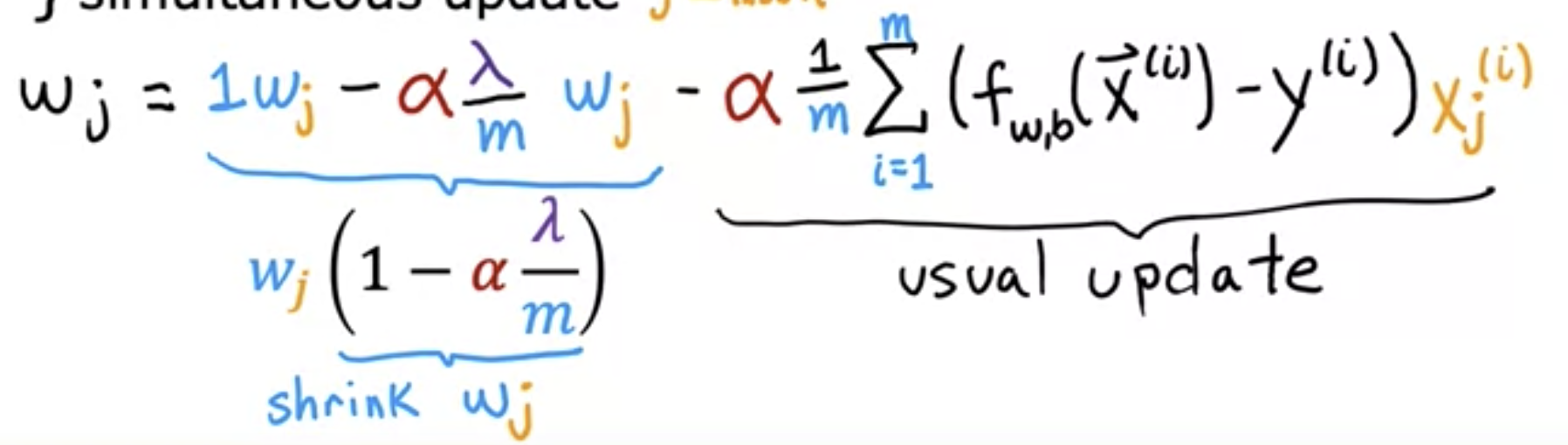
https://youtu.be/jhrrw8Iuus0

람다 수식이 있는 부분을 앞으로 오게 해서, 아래처럼 항을 합쳐보자. 

 

$ wj(1 - a( h / m)) $

 

뒤쪽은 우리가 계산하던 평소의 Gradient Discent이다. 예를 들어 다음과 같은 숫자를 갖고있다고 가정해보자.

a = 0.01 # 알파
labmda = 1 # 람다
m = 50 # 트레이닝 세트 크기

 

그러면 아래와 같은 결과가 나온다

 

$ wj(1 - 0.01(1 / 50)) = wj(1 - 0.0002) = 0.9998 * wj $

 

즉, 매번 계산을 할 때 마다 wj값을 점점 줄여나가는것을 알 수 있다. 이렇게 Regularization은 wj를 점점 줄이는 효과가 있다.

 

 

Reference

https://youtu.be/jhrrw8Iuus0